こんにちは。
2023年12月28日(木)
「最終学歴=中学卒」の魚釣りオジサンの私(55歳)が、独学で「数学検定:準1級」に合格するまでの記録です。

前回 5話では、数学検定1級1次「計算技能検定」に合格するために用意した、表や手帳の事を書きました。
数検1次検定の模範解答には「解法の解説」が無い…。
様々な問題集などで「数検準1級1次検定」に合格するために学習を続け、そして実際に何度も検定を受験しました。

そんな中で、ある1つの困った問題が起きていました。
下の画像は、受験後1ヶ月くらい後に、数検協会から個別成績票と共に郵送されてくる「模範解答」です。画像は1次検定の模範解答です。
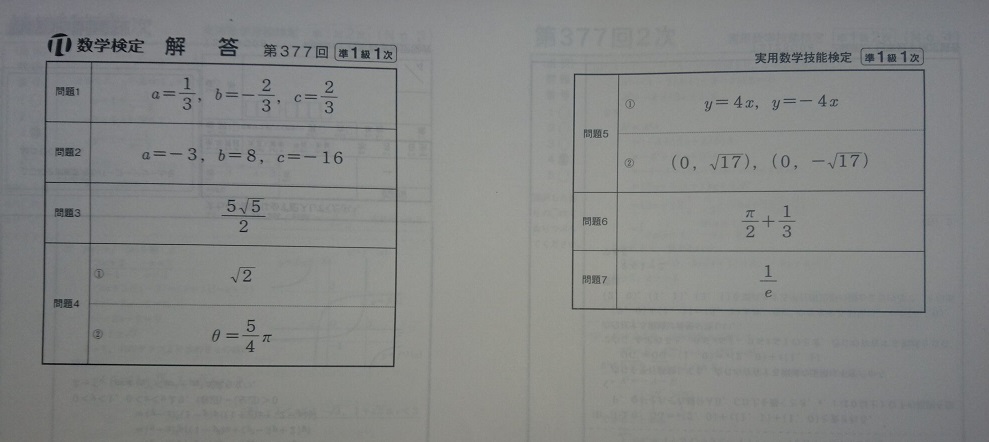
数学検定の1次検定は「計算技能検定」という事もあり、解答用紙には出題の答えのみを書きます。途中の式変形などは記述しません。
よって、数検協会が用意した模範解答にも、解法の途中経過はありません。
計算問題でも解法が分からない場合。
算数・数学の計算問題は「計算の正確性」や「計算スピード」が重視されますが、内容が高度になって来ると計算自体に「解法」が必要になります。
実際に直面した事例として下の問題がありました。

数学Ⅲで学習する『極限』という分野からの出題です。
検定で出題されましたが回答できませんでしたし、後日この問題に取り組んでも解き方が分かりません。

郵送されてきた模範解答には、正解値である「 1/e 」としか書いてありません。
「一体どうやって計算したら、こんな値になるんだ…?」
受験会場で知り合った年配の方に訪ねたりもしましたが、残念ながらその方にも不明でした。
現役の学生さんと違い、私達のような独学の社会人学習者には「指導者」がいません。こんな場面が一番困ります。
そして、数学の学習において必ず避けなければならない行いは「分からない事を解決しないで、そのまま放置する…」事だと思います。
「分からない問題」は、次に同種の問題が検定で出題され時に、また解けない事は明白です。必ず納得するまで理解しておかないとダメでしょう。
「細野真宏」氏の数学参考書との出会い。
検定で出題された『極限』の問題の解法が分からず困っていた時に、大型書店の学習参考書コーナーで下の本を見つけました。
丸々1冊『極限』のみを扱った数学参考書です。細野氏の著書を読んだ事は有りませんでしたが、すぐに購入してその日から読み出しました。
解説がとても丁寧で分かりやすく、理解力が低い私でもドンドンとページが進みます(その後シリーズ全冊購入)。

私的には数学テキストの中では一番のオススメです。

この細野氏の学参シリーズは、かなり以前は違う出版社から発行されていたようです。いわゆるベストセラーですね。現在も小学館から発売中。

元々の原盤が古い参考書なので、現代の洗練された参考書と比べるとかなり「ガサツ」に感じますが、そこがとても親近感をあります。
この参考書で例の『極限』の問題がすぐに解決したのかと言うと、残念がながらそうではありませんでした。
ですが、極限の問題を解くための「ロピタルの定理」というものを知る事ができました。
そして、ついに「あるかたの動画」が参考になり、細野氏の本で紹介されていた『ロピタルの定理』の使用して数検の『極限』の問題の解法が、私にも分かりました。
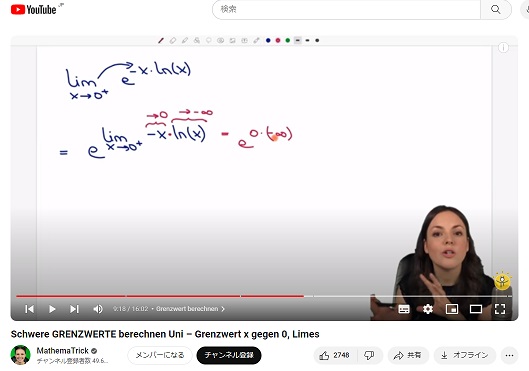
数学動画『MathemaTrick 』。
上の動画はドイツ人(?)の女性が管理している数学の動画チャンネル『MathemaTrick 』です。
もちろん私はドイツ語など喋れませんが、数学の表記はどの国でもほとんど同じです。
ある程度の数学の知識が言葉は分からなくても式変形の流れくらいは理解できるのです。
この動画が始まって9分17秒くらいの所で「ロピタル」という単語が聞き取れます。
「あぁっ!なるほどぉ…。ここで『ロピタルの定理』を使うのかぁっ!」
動画を見終えてから、早速解けなかった数検の『極限』の問題7を解いてみました。

上の汚ったない字で数式が書かれた用紙は、その時の解法の式変形を記述したものです。
これを機会に受験した1次検定の解法は、式変形の流れを全て紙に記述して残す事を習慣にしました。

現時点で解ける問題も、いつ解けなくなってしまうのか自信がありませんからね。